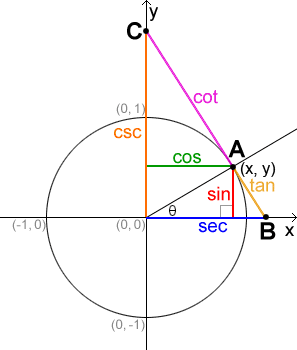
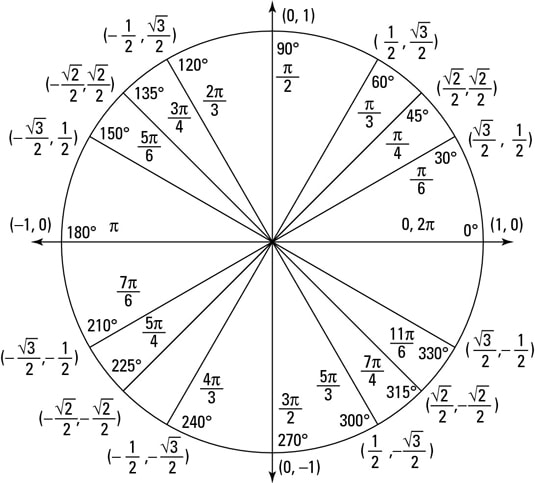
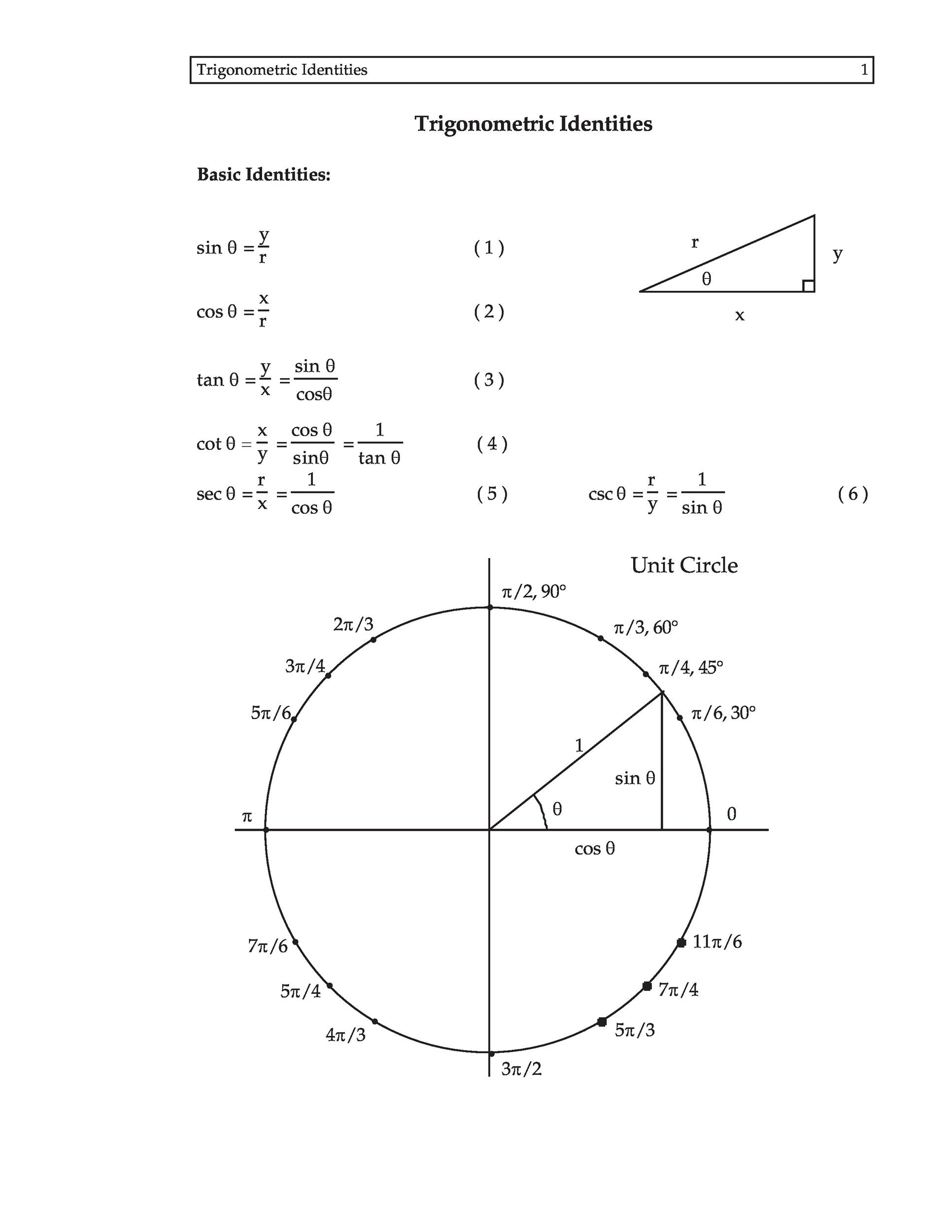
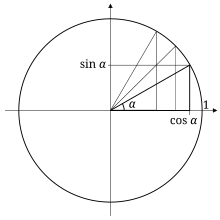
In terms of the unit circle diagram, Just as the sine and cosine can be found as ratios of sides of right triangles, so can the tangent We'll use three relations we already You don't have to remember all this information if you can just remember the ratios of the sides of a 45°45°90° triangle and a 30°60°90° triangleUnit Circle What you just played with is the Unit Circle It is a circle with a radius of 1 with its center at 0 Because the radius is 1, we can directly measure sine, cosine and tangent Here we see the sine function being made by the unit circle Note you can see the nice graphs made by sine, cosine and tangent Degrees and Radians The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of

Sine Wikipedia
Sides of 30 60 90 triangle unit circle
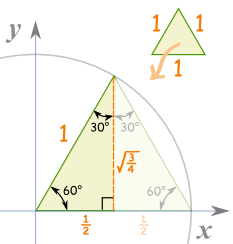
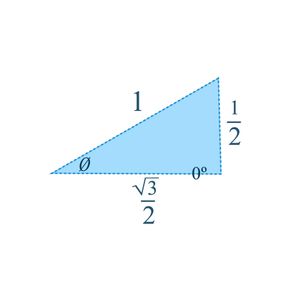
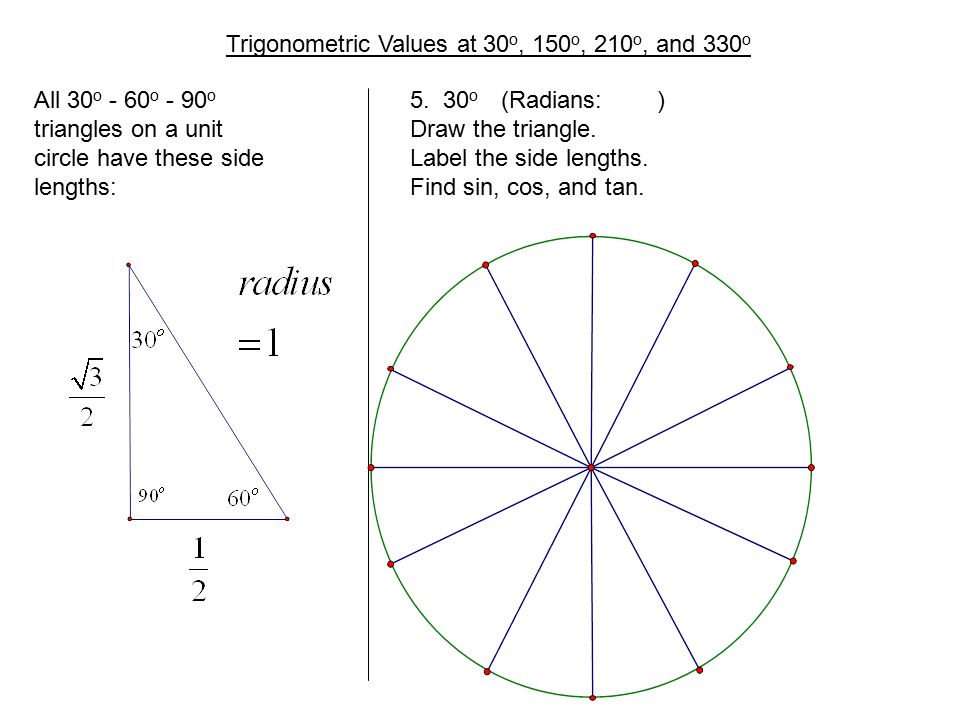
Sides of 30 60 90 triangle unit circle-Ratios Solving Special Triangles The Easy Way You could just get in the habit of always using SohCahToa to find the missing sides of a triangle, but it's not the fastest way In this video, I'll explain how to use ratios (multiplying by root 2, for example) to fill in the missing sides of and trianglesTHE 30°60°90° TRIANGLE THERE ARE TWO special triangles in trigonometry One is the 30°60°90° triangle The other is the isosceles right triangle They are special because, with simple geometry, we can know the ratios of their sides Theorem In a 30°60°90° triangle the sides are in the ratio 1 2 We will prove that below



1
Okay, this is question page 7 87 Question number five Using the unit circle on the 3 60 90 triangle Find any angles Who's tangent is worth three over three, which is opposite over Jason Now, if I go over here to 60 its opposite it through three But it's a Jason does not three, so it can't be that So I am going to do a sneaky thing here I'm going to look at one over Route three, and ifIn conclusion, the unit circle chart demonostrates some properties of the unit circle It results from dividing the circle into and sections respectively Each point from the divisions corresponds to one of the two special triangles 45 45 90 triangle and 30 60 90 triangle30 60 90 triangle area calculator 30 60 90 Right Triangle Side Ratios Expii Product Order Now Since our angles are rigorous there is exactly one type of triangle we could give for any of these starting values 30 60 90 triangle area calculator Enter 1
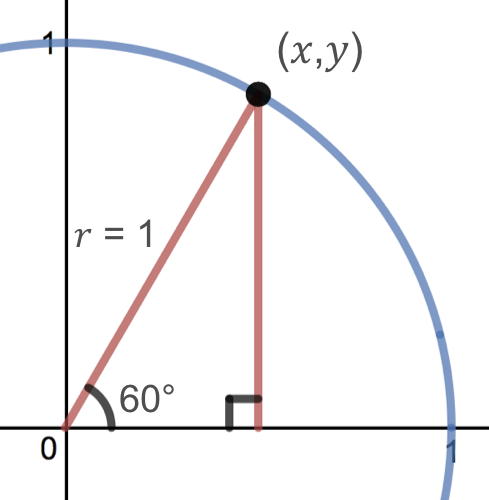
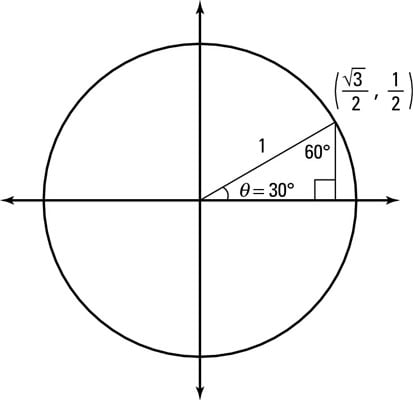
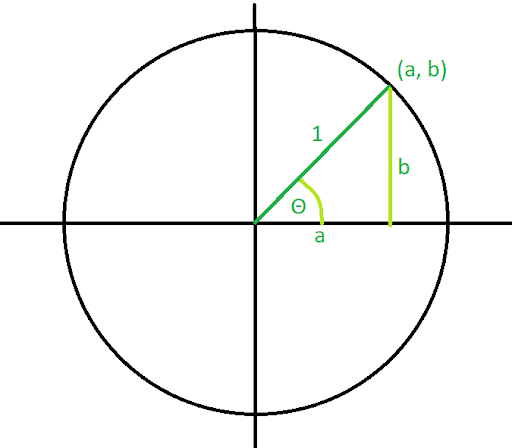
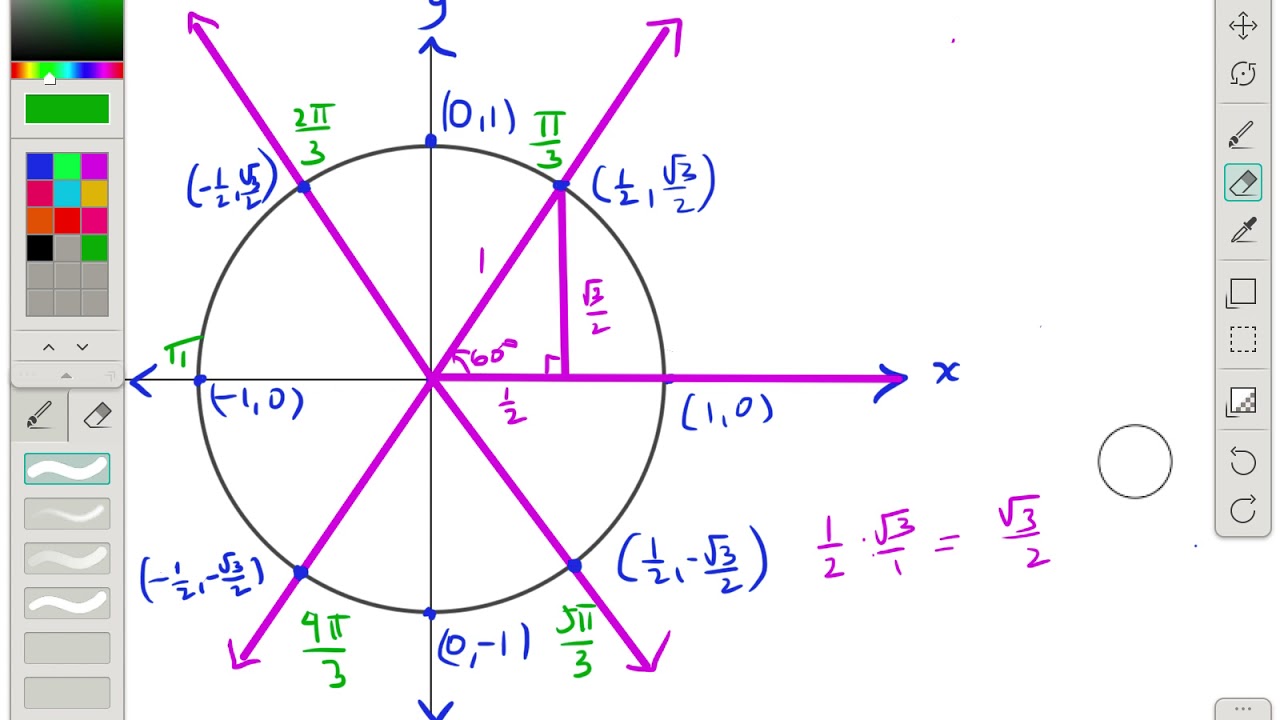
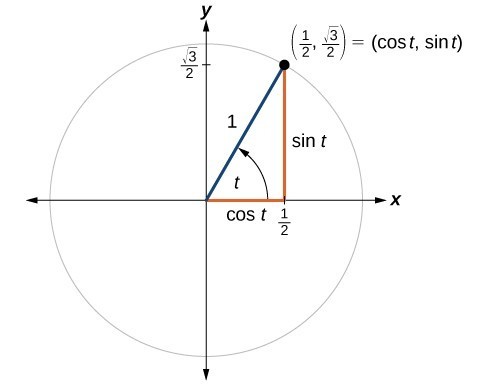
To do this, start by drawing the π/6 angle on your unit circle Remember that special triangles have varying side lengths These are and The short side of the triangle is half of the hypotenuse This means that the ycoordinate is equal to 1/2 On the other hand, the long side is √3 times the shorter side or (√3)/2 A $$ is one of the must basic triangles known in geometry and you are expected to understand and grasp it very easily In an equilateral triangle, angles are equal As they add to $180$ then angles are are all $\frac {180}{3} = 60$ And as the sides are equal all sides are equal (see image) So that is a $$ triangleWhat I have attempted to draw here is a unit a unit circle and the fact that I'm calling it a unit circle means it has a radius of one so this length from the center and I centered it at the origin this length from the center to any point on the circle is of length one so what would this coordinate be right over there right where it intersects along the x axis well it would be X would be one Y
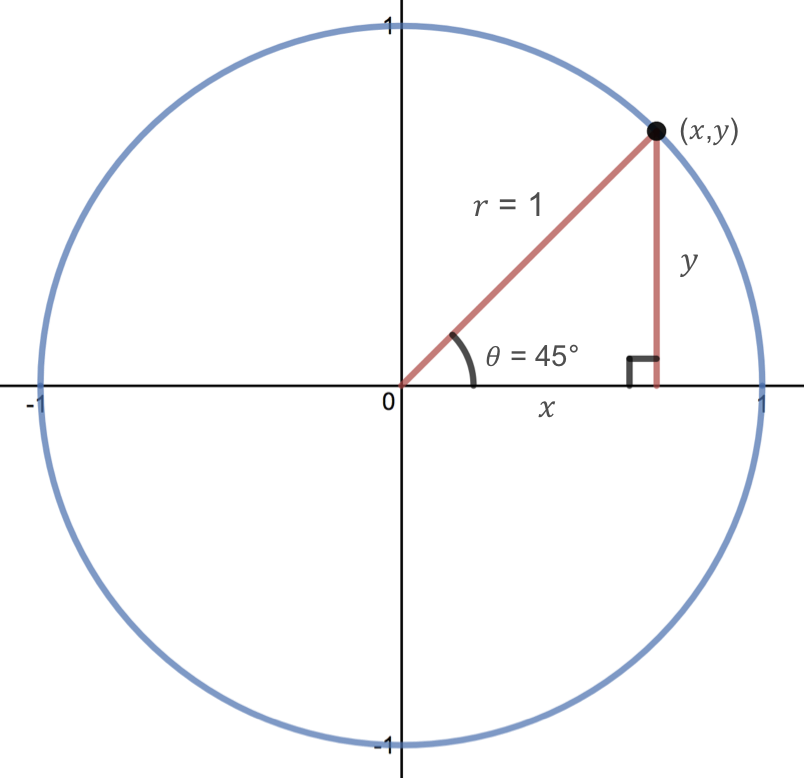
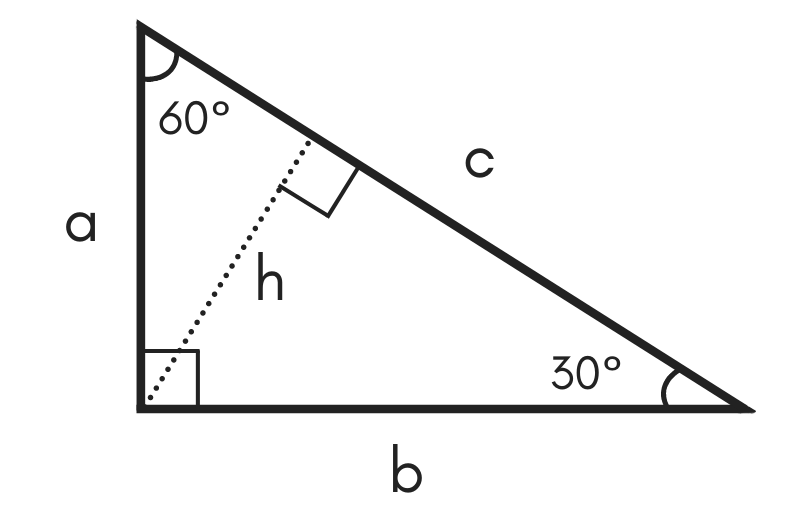
Pythagoras Pythagoras' Theorem says that for a right angled triangle, the square of the long side equals the sum of the squares of the other two sides x 2 y 2 = 1 2 But 1 2 is just 1, so x 2 y 2 = 1 equation of the unit circle Also, since x=cos and y=sin, we get (cos(θ)) 2 (sin(θ)) 2 = 1 a useful "identity" Important Angles 30°, 45° and 60° You should try to remember sinThe triangle The triangle has a right angle (90 ) and two acute angles of 30 and 60 We assume our triangle has hypotenuse of length 1 and draw it on the unit circle Smith (SHSU) Elementary Functions 13 2 / 70 The 30 60 90 triangle Anytime we consider a triangle, we imagine that triangle as half of an equilateral"Anglebased" special right triangles are specified by the relationships of the angles of which the triangle is composed The angles of these triangles are such that the larger (right) angle, which is 90 degrees or π / 2 radians, is equal to the sum of the other two angles The side lengths are generally deduced from the basis of the unit circle or other geometric methods




30 60 90 And 45 45 90 Triangles Youtube




The Unit Circle At A Glance
Triangle Examples There are many times in real life when a situation involves a triangle and there is a need to find the lengths of the sides A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another Although this is true for any angle on the unit circle, most math teachers (and the SAT) focus on the points created by the right triangle and the triangle (using 30 and 60) Since we now have the measure of Θ (either 30, 45, or 60) we can find the cosine and sine for each of these angles according to the unit circle




The Unit Circle At A Glance



Mfg The Unit Circle
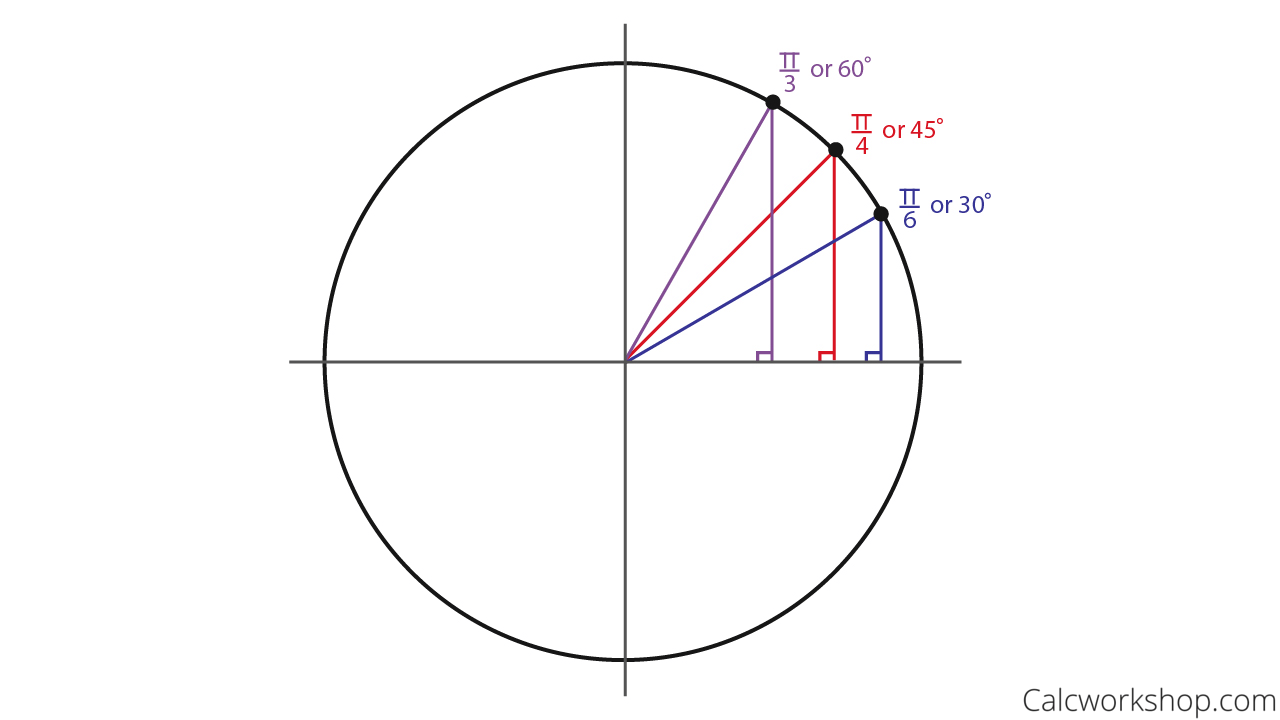
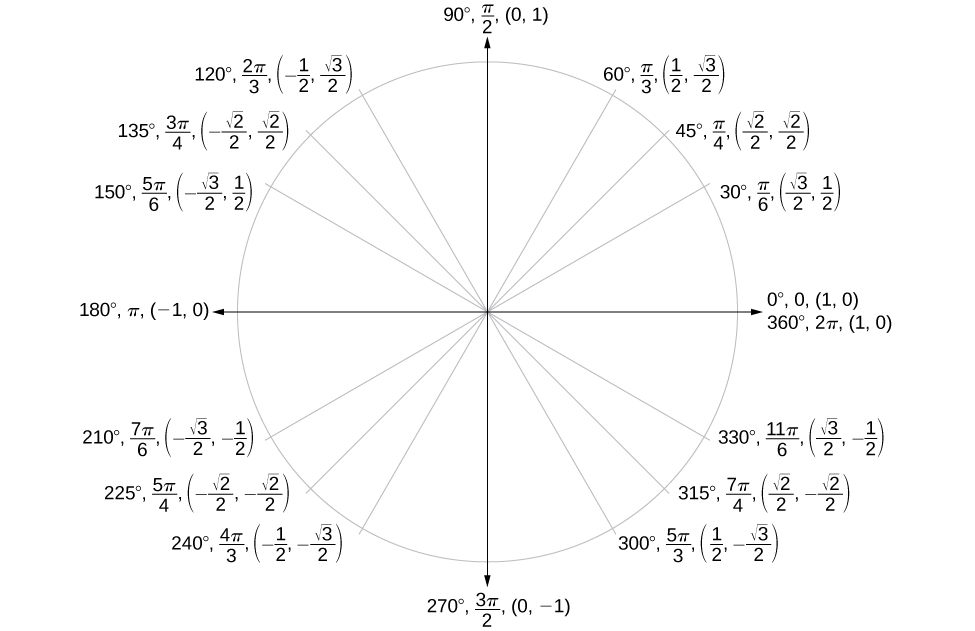
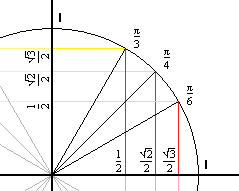
Each blackandred (or blackandyellow) triangles is a special rightangled triangle The figures outside the circle pi/6, pi/4, pi/3 are the angles that the triangles make with the horizontal (x) axis The other figures 1/2, sqrt(2)/2, sqrt(3)/2 are the distances along the axes and the answers to sin(x) (yellow) and cos(x) (red) for each angleThe x and y coordinates of P when θ = 30° using the triangle Therefore, we have two equivalent expressions for the coordinates of P 2 3, cos30 2 1 sin30) 2 1, 2 3 P (cos30 , sin30 ) P (q q q q You should now also be able to find the exact values of sin(60°) and cos(60°) using the triangle and the unit circle IfFinding the coordinates on the unit circle of an angle of 30 degrees using special right triangles



Unit Circle



Mfg The Unit Circle
The Unit Circle The Unit Circle is a circle with a radius of 1 centered at the point (0,0) Moving the green angle slider will rotate the point at (1,0) around the circle in a counterclockwise direction Together with the point at the center of the circle that rotating point forms a right triangle As we move the point between 0 and 90 degrees 30 60 90 Triangle Working Methodology To resolve our right triangle as a 30 60 90, we have to establish very first that the three angles of the triangular are 30, 60, and 90 Resolve for the side sizes;Geometry Unit 4 Lesson 14 CONSTRUCTION OF TRIANGLES Construct right triangles Triangle DEB is an equilateral triangle inscribed in circle A since its three sides are congruent (refer to the ratios between the sides of a triangle), the length of the apothem is 05 times r, or 05rSo,



Unit Circle
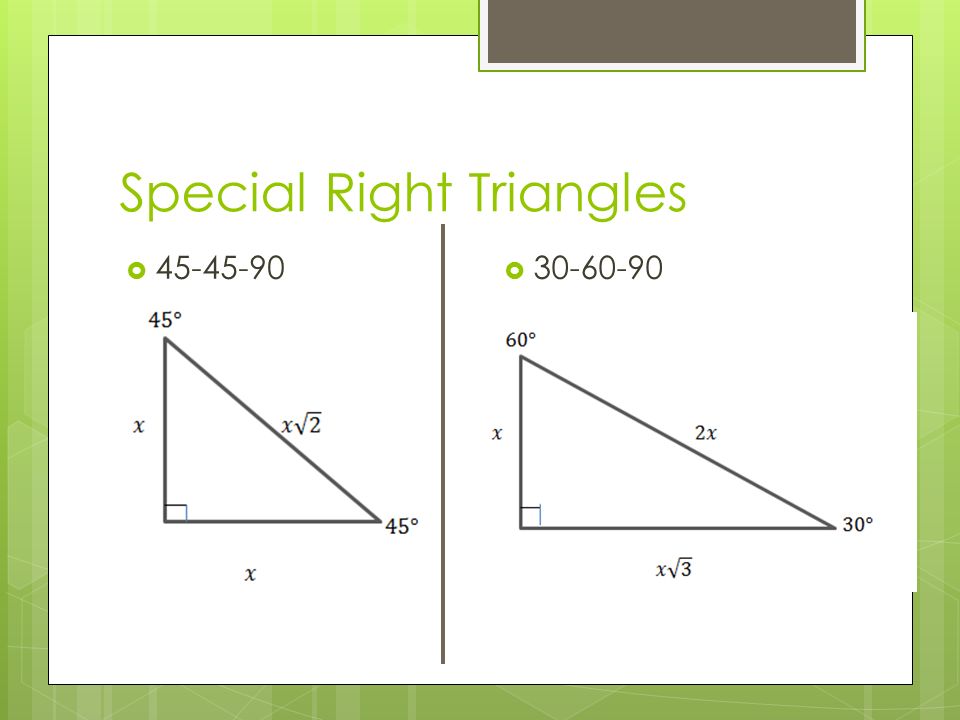



Day 4 Special Right Triangles Angles And The Unit Circle Ppt Download
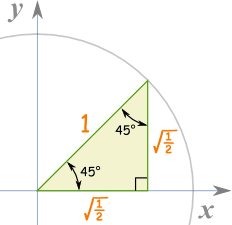
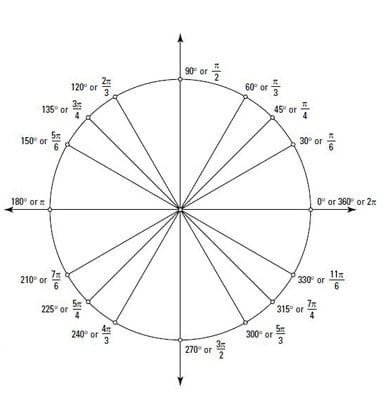
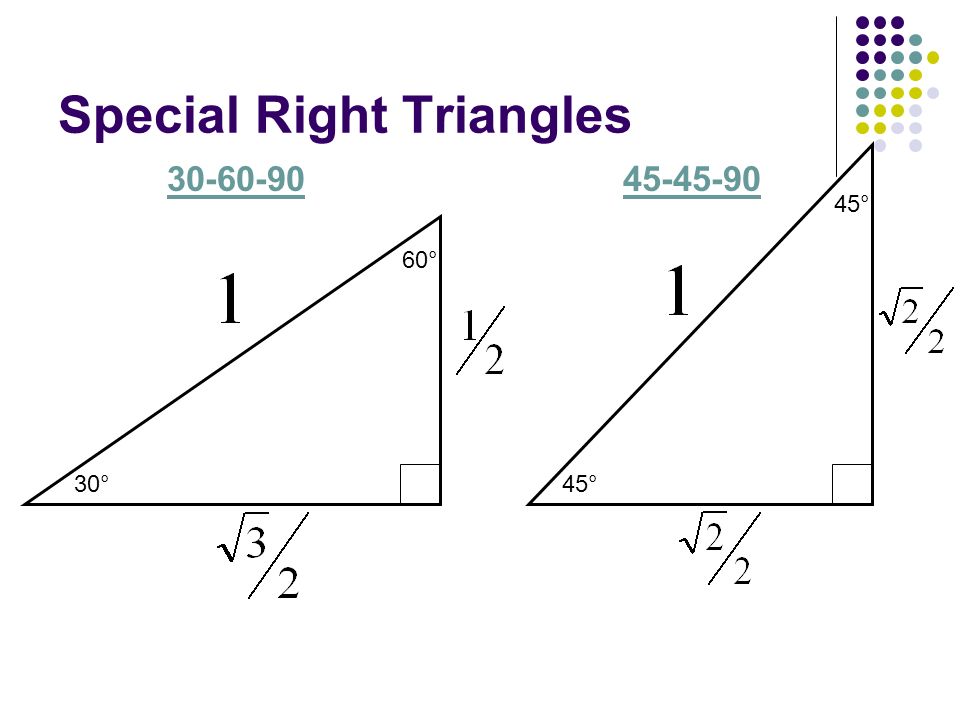
A rightangled triangle containing a 45° angle will be isosceles, so we choose the two shorter sides to be 1 unit in length and use Pythagoras' theorem to find the hypotenuse For the angles 30° and 60°, we start with an equilateral triangle of side 2 unitsThe unit circle that is enclosed between the angle's rays 15 30 45 60 105 90 75 1 135 150 165 180 µ 0 Angle has degree measure µ =45± Protractor º 4 µ Angle has radian measure µ = º 4 Unit Circle Figure 31 Angles can be measured with a protractor Relating the triangle to the Unit Circle Blog Employee training Your guide for training employees online



2
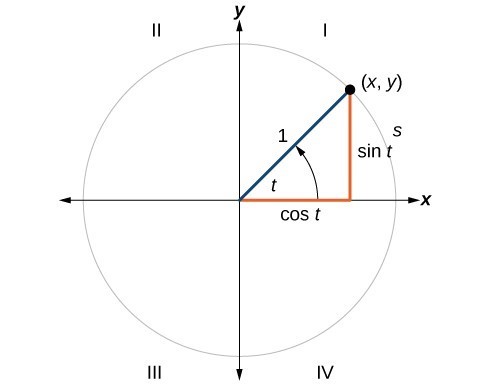



Unit Circle Sine And Cosine Functions Precalculus Ii
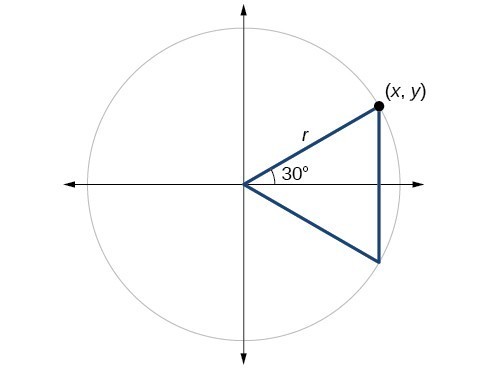
Notice that the above triangle is a 30o60o90o triangle Since the radius of the unit circle is 1, the hypotenuse of the triangle has length 1 Let us call the horizontal side of the triangle x, and the vertical side of the triangle y, as shown below (Only the first quadrant is shown, since the triangle is located in the first quadrant) 130 60 90 triangle sides unit circle The property is that the lengths of the sides of a triangle are in the ratio 12√3 Thus if you know that the side opposite the 60 degree angle measures 5 inches then then this is √3 times as long as the side opposite the 30 degree so the side opposite the 30 degree angle is 5/√3 inches longThe triangle has a right angle (90 ) and two acute angles of 30 and 60 We might assume our triangle has hypotenuse of length 1 and so draw it on the unit circle as in Figure 5, below P(x;y) 1 y 30 x Figure 5 The triangle in the unit circle Anytime we consider a triangle, we really should imagine that triangle as




The Unit Circle Ck 12 Foundation



1
Special Right Triangles and the Unit Circle 15 Feb 191029 AM 30 45 60 90 1 135 150 180 210 225 240 270 300 315 330 360 opposite adjacent hypotenuse x y r sin = y r cos = x r tan = y x And because this is a triangle, and we were told that the shortest side is 8, the hypotenuse must be 16 and the missing side must be $8 * √3$, or $8√3$ Our final answer is 8√3 The TakeAways Remembering the rules for triangles will help you to shortcut your way through a variety of math problems33Provided by the Academic Center for Excellence 3 The Unit Circle Updated October 19 The Unit Circle by Triangles Another method for solving trigonometric functions is the triangle method To do this, the unit circle is broken up into more common triangles the 45°−45°−90° and 30°−60°−90° triangles Some examples of
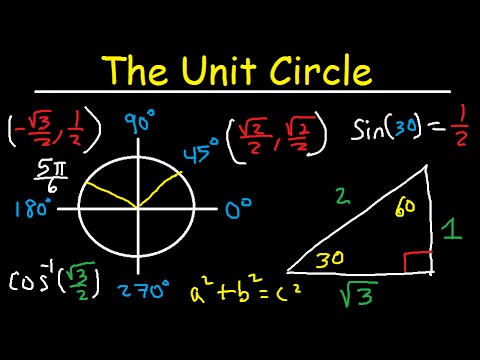



Unit Circle Trigonometry Sin Cos Tan Radians Degrees Youtube
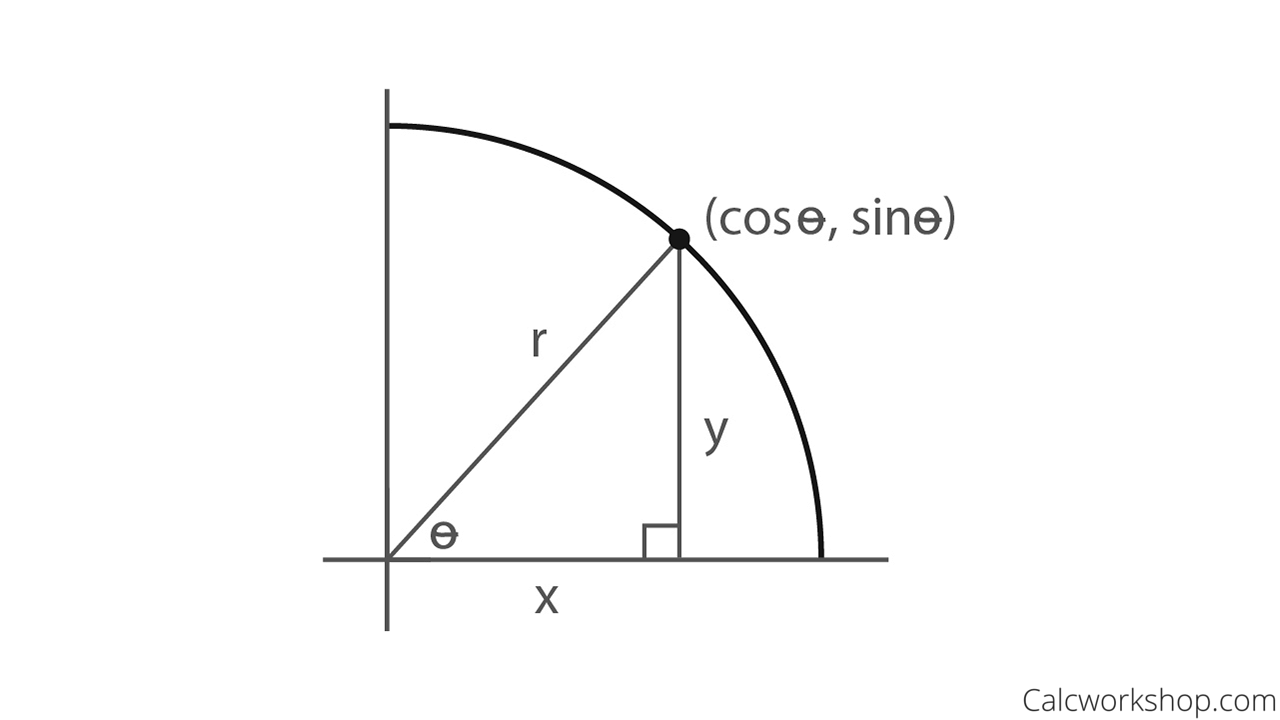



Unit Circle W Everything Charts Worksheets 35 Examples
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2Multiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuse42 Printable Unit Circle Charts Diagrams Sin Cos Tan Cot Etc 30 60 90 Triangle Sides Unit Circle, Unit Circle W Everything Charts Worksheets 35 Examples Exact Trig Values
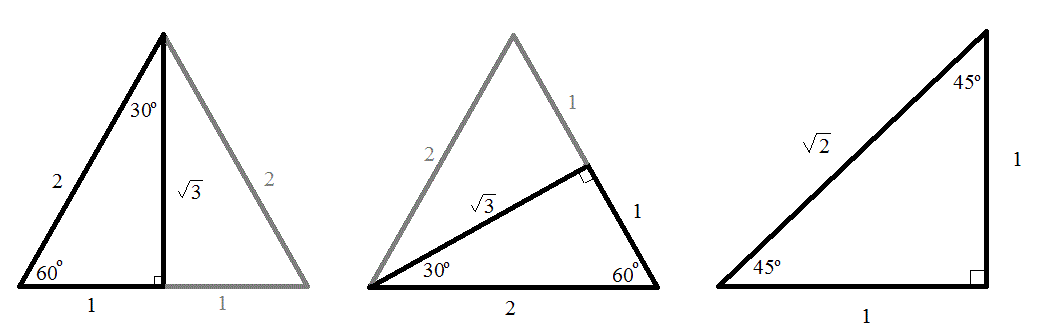



How Do You Find Trigonometric Ratios Of 30 45 And 60 Degrees Socratic




Unit Circle With A 30 60 90 Right Triangle Youtube
Special Right Triangles Formulas 30 60 90 And 45 45 90 Special 30 60 90 Triangle Calculator, Unit Circle Table Of Values Mathematics Stack Exchange Triangle Calculator30 60 90 Triangle, 30 60 90 triangle theorem > ONETTECHNOLOGIESINDIA, Triangle 30 60 90 ClipArt ETC, Triangle AdvanteX SUV TR259 Tyre Tests and Reviews, One angle of rhombus is given to be 60 degrees and itsA triangle is a right triangle where the three interior angles measure 30 °, 60 °, and 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that




How To Work With 30 60 90 Degree Triangles Education Is Around



How To Plot The Major Angles Of The Whole Unit Circle Dummies
Triangle In the above diagram notice how the horizontal side of the triangle is labeled 'x' and the vertical side labeled 'y' is another tool that we use in Trigonometry that makes finding values of trig functions manageable it is called the UNIT CIRCLEExample of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units inA minimum of 1 side size has to be already understood If we know that we are collaborating with an appropriate triangle, we understand that




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube



Unit Circle W Everything Charts Worksheets 35 Examples
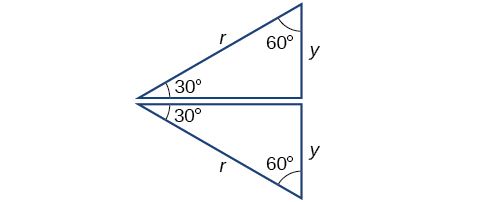
30 60 90 triangle sides unit circle Start studying Unit circle Learn vocabulary, terms, and more with flashcards, games, and other study tools Search Create The output is the ratio between 2 sides of a right triangle 30° 60° 90° In conclusion, the unit circle chartThe 30° 60° 90° triangle is seen below on the left Next to that is a 30° angle drawn in standard position together with a unit circle The two triangles have the same angles, so they are similar Therefore, corresponding sides are proportional The hypotenuse on the right has length 1 (because it is a radius)A right triangle (or perhaps we should say a right triangle) has a ratio of , corresponding to the sides opposite The hypotenuse is 1, so That gives us for , and for Now we can talk about what all this stuff means You didn't think we'd really hold out on you?



The Trig Functions Are About Multiplication Making Your Own Sense



Content The Trigonometric Ratios
For 4 Triangles, click on the link to the left A Triangle looks like the one below When using a Triangle, the following formula/model is used to solve problems dealing with finding the other sideHere use an equilateral triangle with unit sides That is From AMB (right angled) Then from the fig above Sin 30 0 = = A unit circle is a circle with radius (1 unit) Suppose p(x,y) is a point in a unit circle 30° 60° = 90Pshaw Take a look at the special right triangles
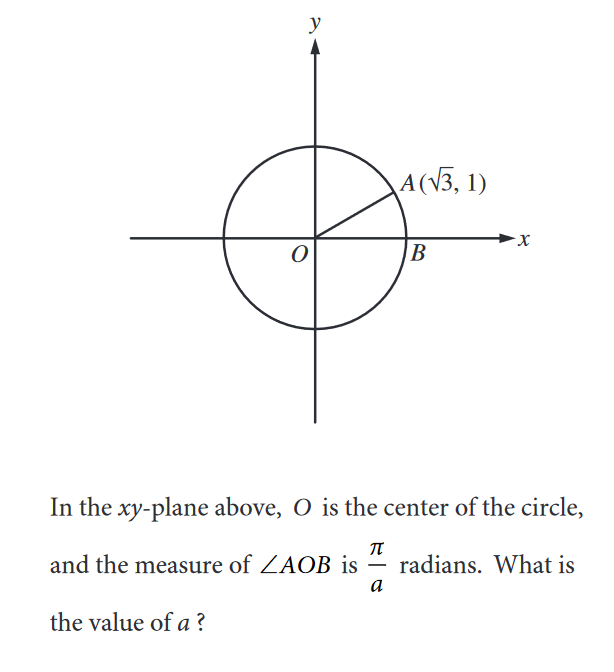



The Unit Circle What You Need To Know For The Sat



C330 Trig Functions Tan Gents And Other Things Of Interest
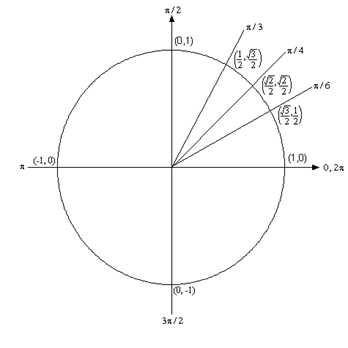



Algebra Trig Review




30 60 90 Triangles Special Right Triangle Trigonometry Youtube
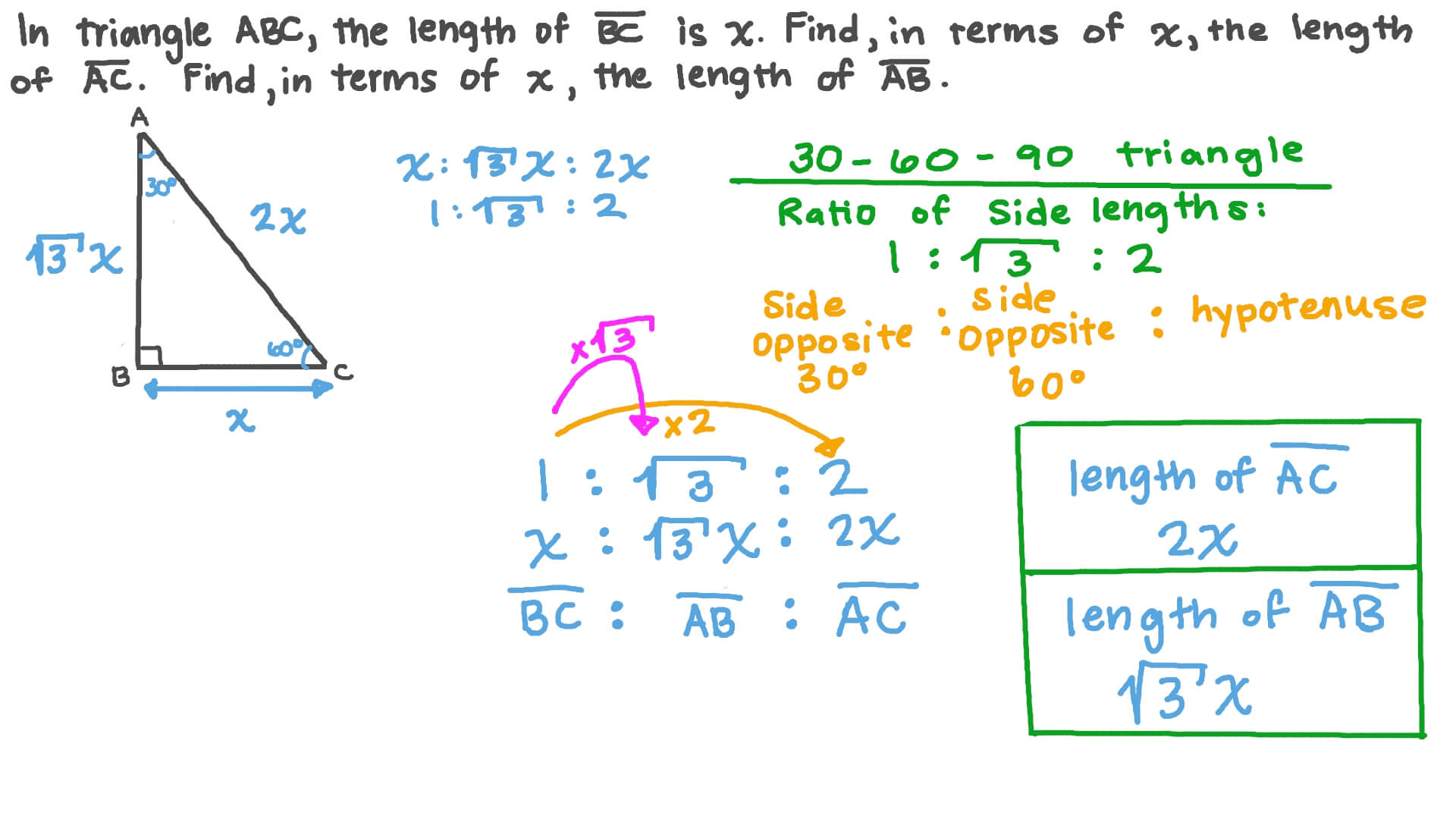



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa




How To Find Exact Values Of Sine Cosecant Using The Unit Circle Special Triangles Algebra Study Com
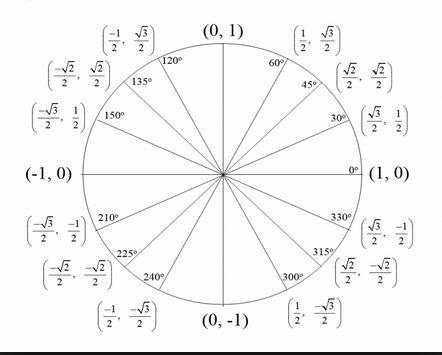



How Do You Create A 16 Point Unit Circle That Ranges From 0 To 8pi Socratic



Unit Circle Trigonometry Learning Objective S Understand Unit Circle Reference Angle Terminal Side Standard Position Find The Exact Trigonometric Function Values For Angles That Measure 30 45 And 60 Using The Unit Circle Find The Exact



30 60 90 Special Right Triangle Calculator Inch Calculator



1




Trigonometry Snow Mountain



42 Printable Unit Circle Charts Diagrams Sin Cos Tan Cot Etc




Sine Wikipedia



1




4 Special Triangles And The Unit Circle No Chegg Com




30 60 90 Unit Circle Youtube



5 2 Unit Circle Sine And Cosine Functions Mathematics Libretexts



Unit Circle
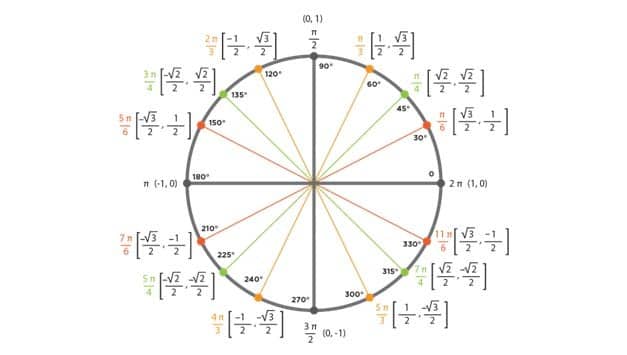



Unit Cricle Chart Brief Explanation Of Unit Circle Chart Trig Identities



Unit Circle Chart




File Unit Circle Angles Svg Wikimedia Commons
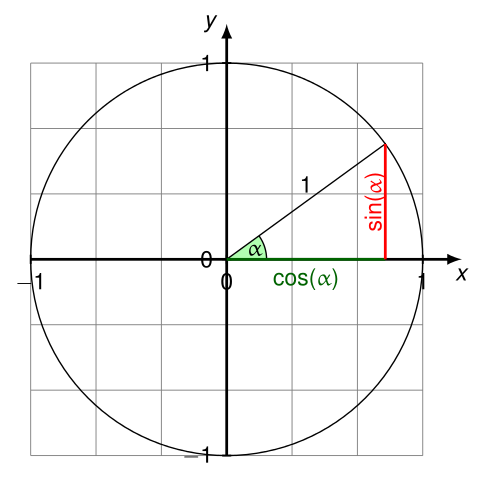



3 Expert Tips For Using The Unit Circle




Trigonometry
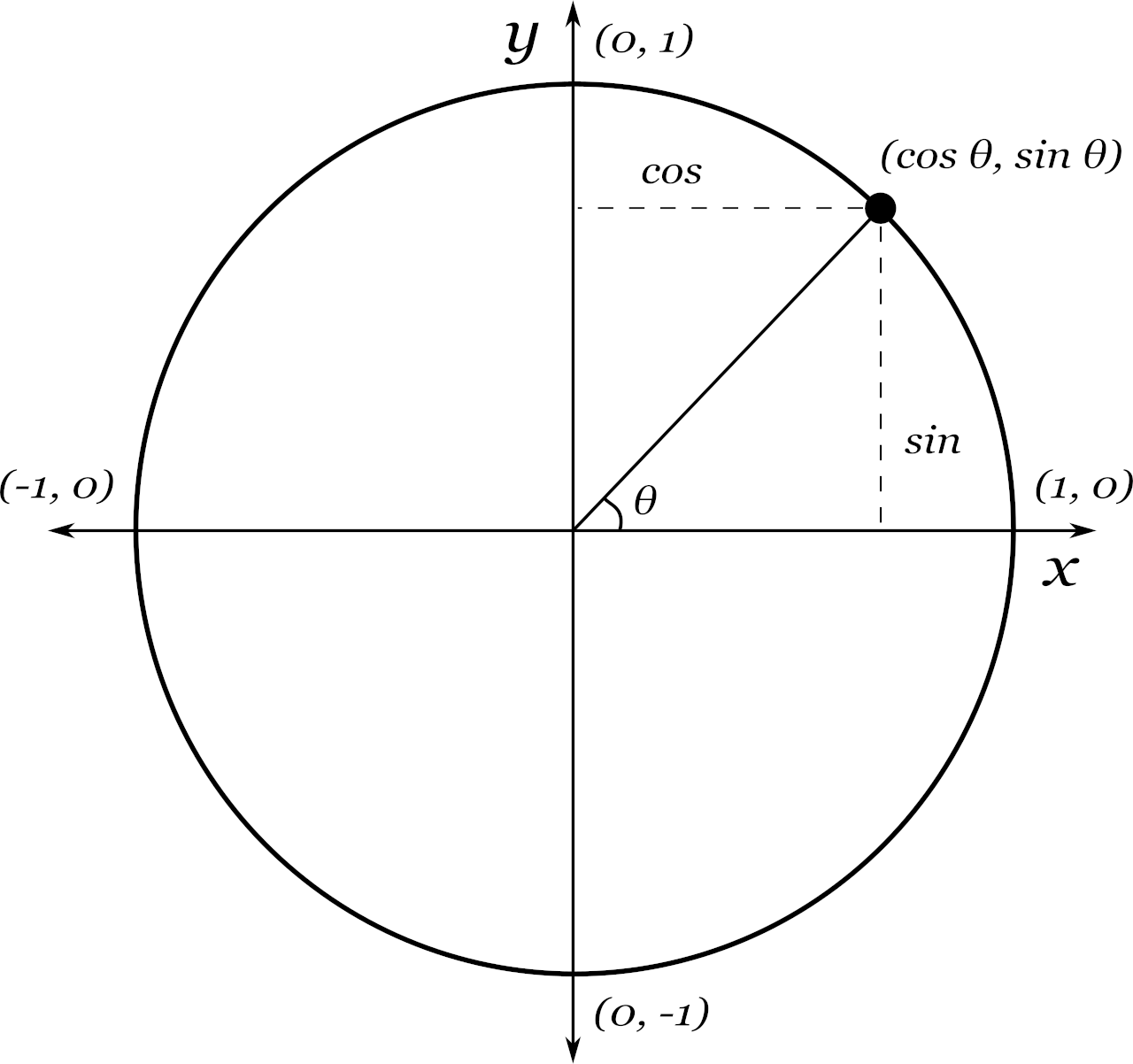



Unit Circle Calculator Inch Calculator



30 60 90 Degree Triangle Shefalitayal




The Unit Circle Ck 12 Foundation




Unit Circle
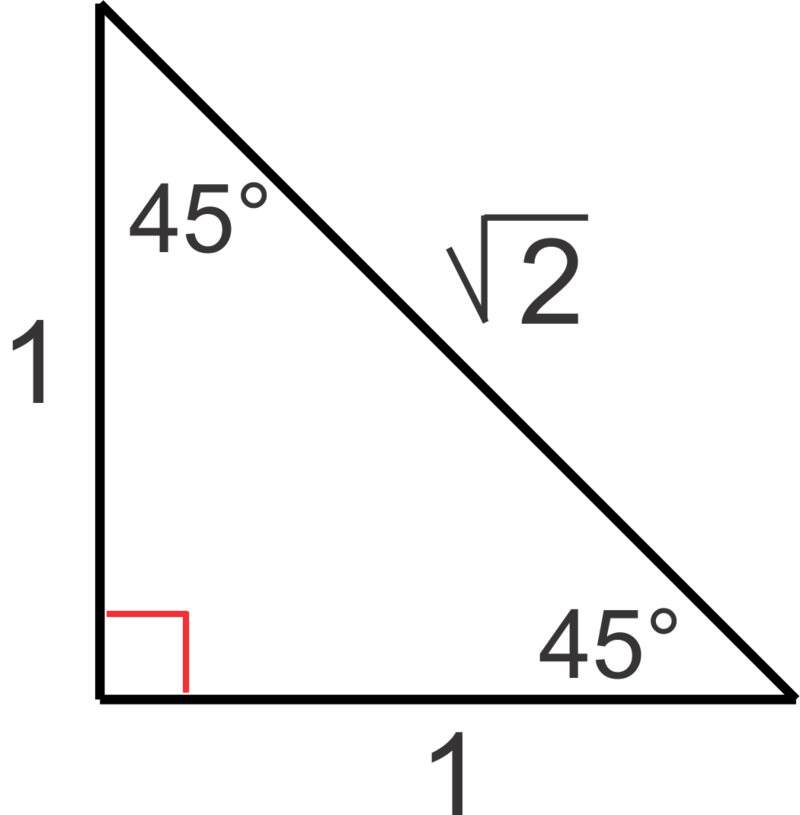



Trigonometric Ratios On The Unit Circle Ck 12 Foundation



How Do The Special Right Triangles Relate To The Unit Circle Socratic




Unit Circle



What Is The Unit Circle Expii



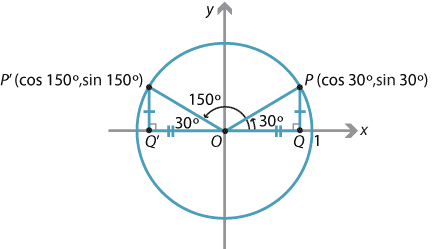
If You Have To Find Cos 150 On The Unit Circle Would It Be Easier To Convert It To Sin 90 150 Quora




Sine Wikipedia



Unit Circle




The Unit Circle At A Glance



Unit Circle Sine And Cosine Functions Precalculus Ii



Unit Circle Trigonometry Learning Objective S Understand Unit Circle Reference Angle Terminal Side Standard Position Find The Exact Trigonometric Function Values For Angles That Measure 30 45 And 60 Using The Unit Circle Find The Exact




30 60 90 Triangle
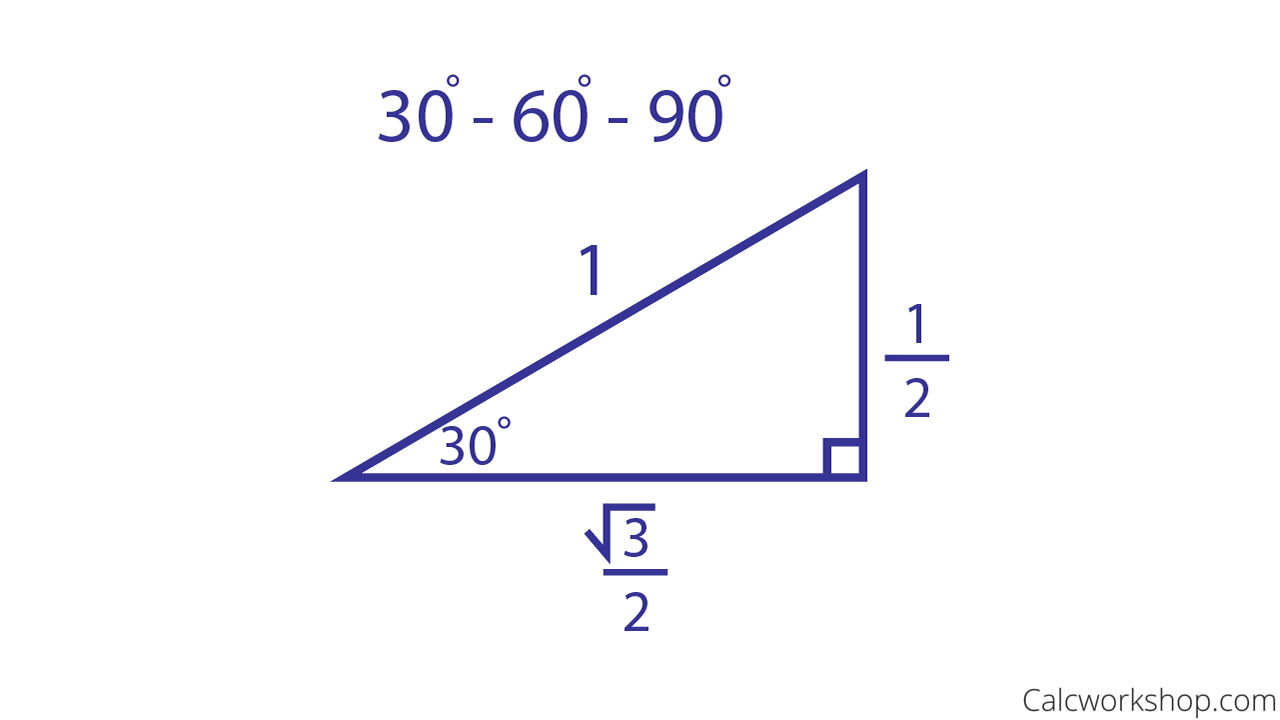



Unit Circle W Everything Charts Worksheets 35 Examples




Unit Circle



Positive And Negative Angles On A Unit Circle Dummies



The Unit Circle What You Need To Know For The Sat




The Unit Circle Ck 12 Foundation



Trig 1 26 Introduction To The Unit Circle Part 4 60 30 90 Triangle Youtube



30 60 90 Triangle Unit Circle Shefalitayal




How To Use The Special Right Triangle 30 60 90 Studypug



Trigonometry



How To Use The Unit Circle In Trig Howstuffworks




Unit Circle



4 2 Day 1 Trigonometric Functions On The Unit Circle Pg 472 6 10 Evens Evens 46 54 56 60 For Each Question Except The 0 O 90 O 180 O Ppt Download



Trigonometric Ratios In The Unit Circle 6 December Ppt Download
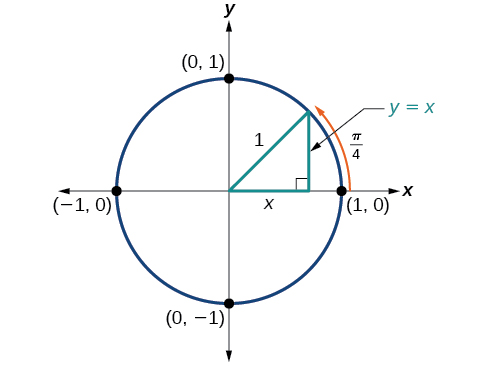



5 2 Unit Circle Sine And Cosine Functions Mathematics Libretexts



1



Unit Circle Trigonometry Degrees Intomath



42 Printable Unit Circle Charts Diagrams Sin Cos Tan Cot Etc




Unit Circle Quick Lesson Downloadable Pdf Chart Matter Of Math




Unit Circle Rmhs Mathematics Ms Stevenson Room 603
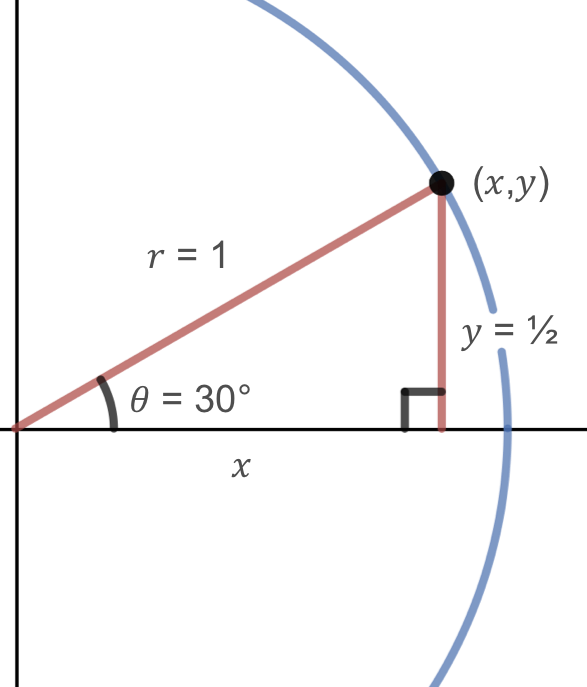



Mfg The Unit Circle
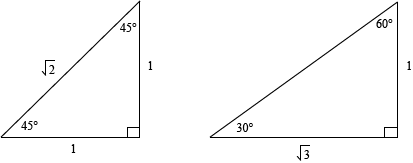



The Unit Circle At A Glance



How To Create A Simple Program About The Unit Circle Quora




The Complete Guide To The 30 60 90 Triangle
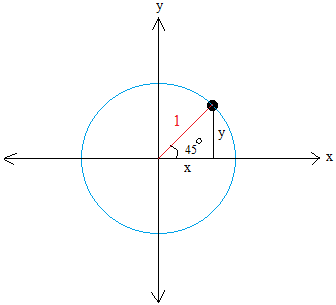



Using The Unit Circle To Find Sin 45 Degrees



2
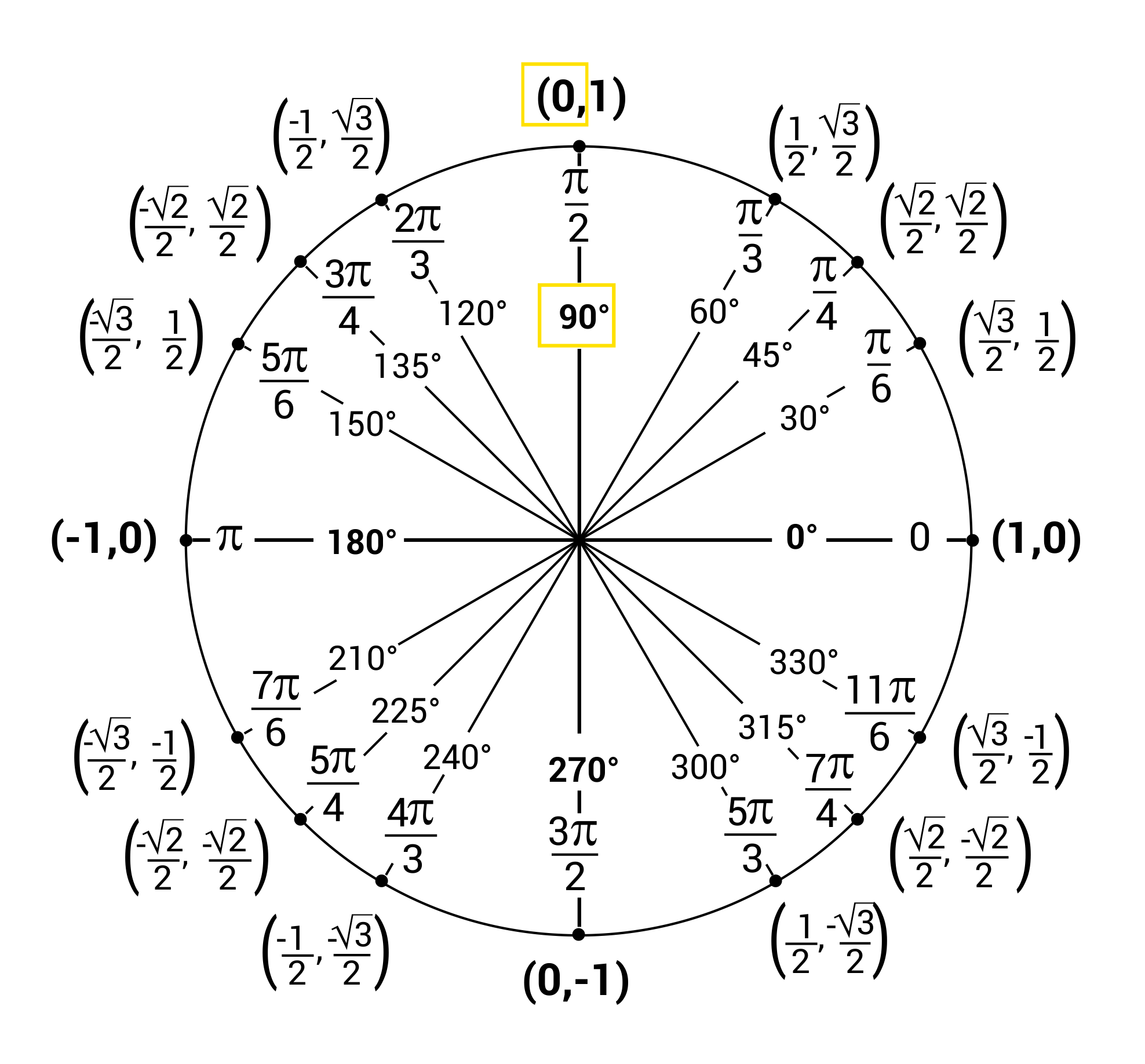



Unit Circles And Standard Position Video Practice




The Unit Circle Ck 12 Foundation
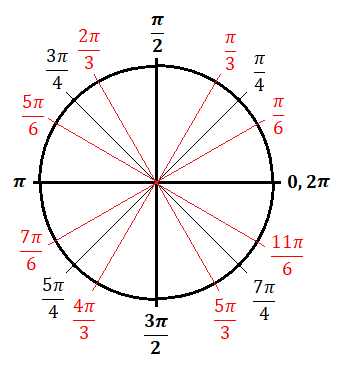



3 Expert Tips For Using The Unit Circle




Solved 4 Using Symmetry Determine The Coordinates Of The Chegg Com




Section 3 2 Unit Circles With Sine And Cosine Ppt Download




Unit Circle Quick Lesson Downloadable Pdf Chart Matter Of Math




Solved 4 Using Symmetry Determine The Coordinates Of The Chegg Com




7 There Is One More Triangle To Place We Will Place Chegg Com
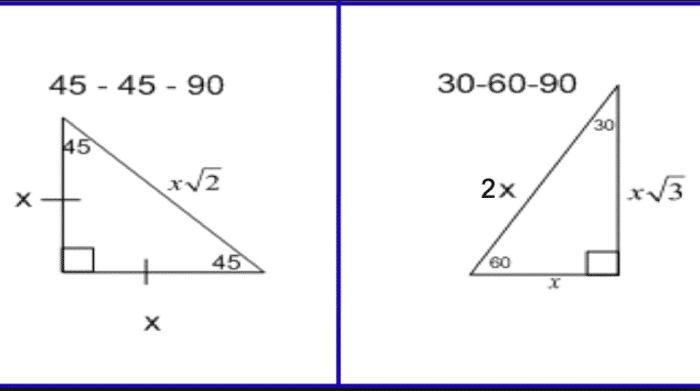



Special Right Triangles Complete Reference Guide The Education
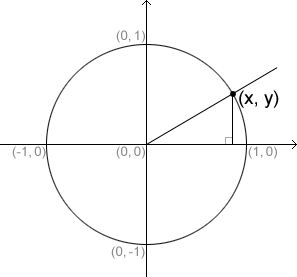



Unit Circle
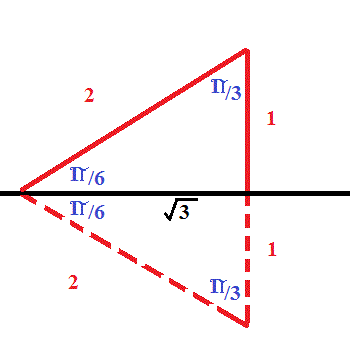



How Do You Find The Exact Values Sin Pi 6 Using The Special Triangles Socratic
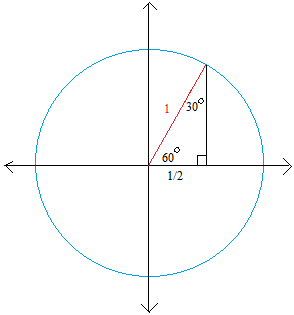



How To Find Sine And Cosine Using The Unit Circle
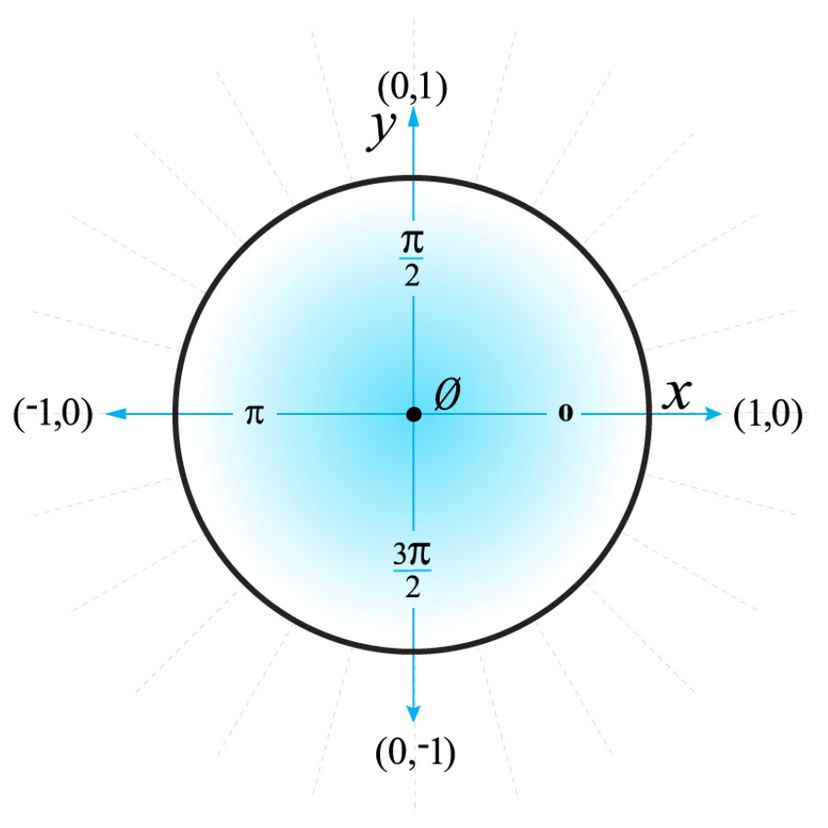



How To Use The Unit Circle In Trig Howstuffworks



Special Right Triangle Wikipedia



Unit Circle Sine And Cosine Functions Precalculus Ii



Unit Circle Algebra And Trigonometry



Special Angles In The Unit Circle



2




Trigonometric Ratios On The Unit Circle Ck 12 Foundation



0 件のコメント:
コメントを投稿